Speculative decoding for LLM inference

Speculative decoding is a neat trick that provides significant speedups to LLM inference. This post was originally inspired by this Karpathy tweet – I will discuss how the algorithm works in more detail and prove its correctness.

The idea is based on the following facts:

• LLM inference for batch size $k$ takes approximately the same time as inference for batch size $1$, for surprisingly large values of $k$. In particular, for low batch sizes, LLMs are bound by memory-bandwidth.
• Many tokens at inference time are easy, and can be predicted by a cheap model. For example, predicting for i in range(N) in Python code, or predicting articles like the or a required for grammatical correctness.

The main algorithm does the following:

• Sample a candidate sequence of $K$ tokens from a smaller cheap model.
• Run the cheap model’s predictions through the main model with batch size $K$ to obtain logits.
• Skip forward through all tokens that agree with the draft model. Once we hit a disagreement with the target model, throw the remaining draft tokens away and repeat.

Here’s an example of what this looks like in practice:

💬 Image from Leviathan et al. 2023.

Inference Speed Ups #

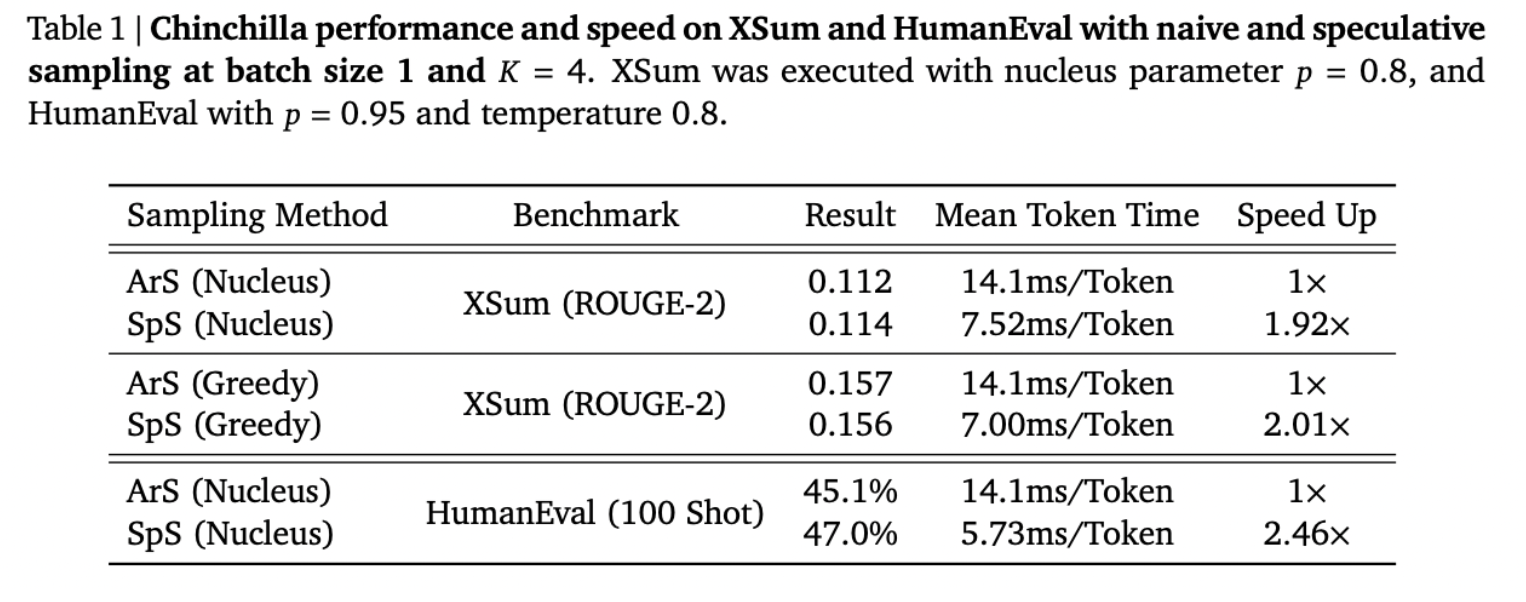
Chen et al. 2023 tried this technique on Chinchilla 70B. They find an approximate speedup of 2x, which is a massive improvement. Interestingly, the speedup differs by domain, because different domains have different frequencies of “easy tokens.” The speedup on HumanEval (code generation) is greater than the speedup on XSum (text summarization), which suggests that code tends to have more easy tokens than text.

Precursor: LLMs are bound by memory-bandwidth at inference time #

Below is the hierarchy of memory on a system with a CPU and A100 GPU. 💬 Image from the FlashAttention paper, Dao et al. 2022.

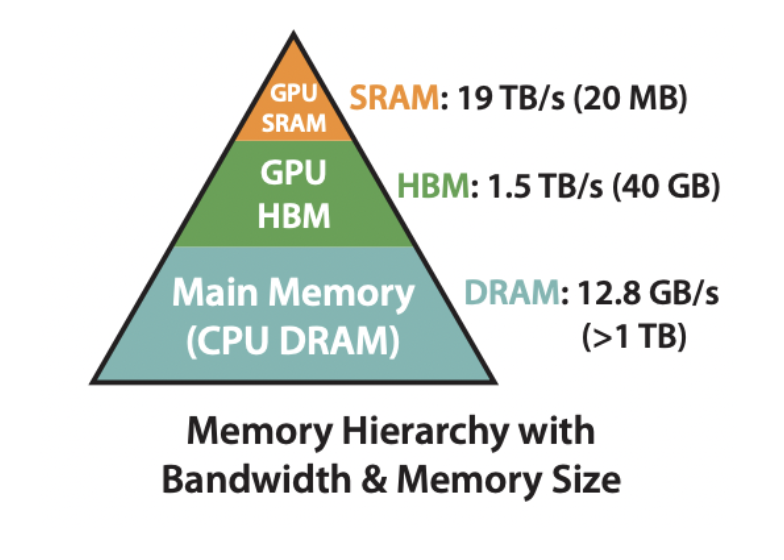
The key mental model for GPUs is that we need to move data from high-bandwidth memory (HBM) to static random-access memory (SRAM), where computation occurs. Some relevant stats for an A100-40GB are below. As can be seen, GPU compute has grown significantly faster than memory bandwidth.

• HBM: 40GB
• SRAM: 20MB
• Memory bandwidth: 1935 GB/s
• Compute: 312 TFLOPS with FP16

This post does analysis that breaks down the latency incurred by memory-bandwith and by compute. Let $P$ be the number of parameters in a language model. Let $n_{\text{bytes}}$ denote the number of bytes in each parameter (16 for FP16, 8 for INT8, etc.) Let $B$ be the batch size. It turns out we can express the latency incurred by compute and memory bandwidth as follows:

$$ \begin{aligned} \text { latency }_{\text {model }} & =\max \left(\text { latency }_{\text {compute }}, \text { latency }_{\text {memory }}\right) \\ \text { latency }_{\text {memory }} & =\frac{2 \cdot P \cdot n_{\text {bytes }}}{n_{\text {memory bandwidth }}}, \\ \text { latency }_{\text {compute }} & =\frac{2 \cdot P \cdot B}{n_{\text {flops }}}\end{aligned} $$

Plugging in the above values for memory bandwidth and FLOPs, Finbarr Timbers concludes that memory bandwidth dominates compute latency for batch sizes smaller than 161.

Going through the algorithm in detail #

The two main references that describe speculative decoding are Chen et al. 2023 and Leviathan et al. 2023. I will focus on the presentation in the first paper as I found it easier to read.

The algorithm works as follows.

Algorithm – Speculative Decoding

Inputs:

• High latency target model $q$.
• Low latency draft model $p$.
• Initial prompt $x_0, \dots, x_t$.
• Lookahead $K$.
• Minimum target sequence length $T$.

In the above algorithm, the $+$ subscript denotes the following operation:

$$ (f(x))_{+}=\frac{\max (0, f(x))}{\sum_x \max (0, f(x))} $$

Proof of correctness #

Let’s prove Theorem 1 from the paper, which states the following. This is important to demonstrate correctness of the algorithm.

Theorem 1. Speculative decoding recovers the target model’s probability distribution $q(x)$.

As above, let $p$ be the draft model, and $q$ be the target model. Let $X$ be the final sample produced by the algorithm above. We will show that $P(X = x)$ is equal to $q(x)$.

The first step is to break $P(X = x)$ into two cases. Either $\tilde{x} = x$ and we accept the draft sample, or we reject it and resample.

So we can write:

$$ \begin{aligned} P(X = x) &= P(\tilde{x} = x) P(\tilde{x} \text{ accepted} | \tilde{x} = x) + P(\tilde{x} \text{ rejected}) P(X = x | \tilde{x} \text{ rejected}) \end{aligned} $$

Let’s calculate each of the two terms. We will start with the acceptance probability.

$$ \begin{aligned} P(\tilde{x} = x) P(\tilde{x} \text{ accepted} | \tilde{x} = x) &= p(x) \min \left ( \frac{q(x)}{p(x)}, 1 \right ) \\ &= \min ( p(x), q(x)), \end{aligned} $$

where we have used the fact that we can multiply through the $\min$ operator.

For the next term, we can calculate as follows: $$ \begin{align} P(\tilde{x} \text { rejected})&=1-P(\tilde{x} \text { accepted}) \\ &=1-\sum_{x^{\prime}} P\left(X=x^{\prime}, \tilde{x} \text { accepted}\right) \\ &=1-\sum_{x^{\prime}} \min \left(p\left(x^{\prime}\right), q\left(x^{\prime}\right)\right) \\ &=\sum_{x^{\prime}} q\left(x^{\prime}\right)-\min \left(p\left(x^{\prime}\right), q\left(x^{\prime}\right)\right) \\ &=\sum_{x^{\prime}} \max \left(0, q\left(x^{\prime}\right)-p\left(x^{\prime}\right)\right) \end{align} $$

Also, from the algorithm above, we have that: $$ P(X = x | \tilde{x} \text{ rejected}) = \frac{\max(0, q(x) - p(x))}{\sum_{x'} \max \left( 0, q(x') - p(x') \right)} $$

Multiplying through, we have:

$$ \begin{align} & P(\tilde{x} = x) P(\tilde{x} \text{ accepted} | \tilde{x} = x) + P(\tilde{x} \text{ rejected}) P(X = x | \tilde{x} \text{ rejected}) \\ &= \min (p(x), q(x)) + \left ( \frac{\max(0, q(x) - p(x))}{\sum_{x'} \max \left( 0, q(x') - p(x') \right)} \right ) \sum_{x^{\prime}} \max \left(0, q\left(x^{\prime}\right)-p\left(x^{\prime}\right)\right) \\ &= \min (p(x), q(x)) + \max (0, q(x) - p(x)) \\ &= q(x). \end{align} $$

This finishes the proof of Theorem 1.

Thanks to Kevin Chen and Andy Chen for reading drafts of this post.